User-defined kernels

Introduction

One of the most significant benefits of the fcmc package is that it allows creating personalized kernel functions. fmcmc_kernel objects are built with the kernel_new function (a function factory) and require (at least) one parameter, the proposal function. In what follows, we show an example where the user specifies a transition kernel used to estimate an integer parameter, the n parameter of a binomial distribution.

Size parameter in a binomial distribution

Imagine that we are interested in learning the size of a population given an observed proportion. In this case, we already know about the prevalence of a disease. Furthermore, assume that 20% of the individuals acquire this disease, and we have a random sample from the population $y \sim \mbox{Binomial}(0.2, N)$. We don’t know $N$.

Such a scenario, while perhaps a bit uncommon, needs special treatment in a Bayesian/MCMC framework. The parameter to estimate is not continuous, so we would like to draw samples from a discrete distribution. Using the “normal” (pun intended) transition kernel may still be able to estimate something but does not provide us with the correct posterior distribution. In this case, a transition kernel that makes discrete proposals would be desired.

Let’s simulate some data, say, 300 observations from this Binomial random variable with parameters $p = .2$ and $N = 500$:

library(fmcmc)
set.seed(1) # Always set the seed!!!!

# Population parameters
p <- .2
N <- 500

y <- rbinom(300, size = N, prob = p)

Our goal is to be able to estimate the parameter $N$. As in any MCMC function, we need to define the log-likelihood function:

ll <- function(n., p.) {
  sum(dbinom(y, n., prob = p., log = TRUE))
}

Now comes the kernel object. In order to create an fmcmc_kernel, we can use the helper function kernel_new as follows:

kernel_unif_int <- kernel_new(
    proposal = function(env) env$theta0 + sample(-3:3, 1),
    logratio = function(env) env$f1 - env$f0 # We could have skipped this
    )

Here, the kernel is in the form of $\theta_1 = \theta_0 + R, R\sim \mbox{U}\{-3, ..., 3\}$, this is, proposals are done by adding a number $R$ drawn from a discrete uniform distribution with values between -3 and 3. While in this example, we could have skipped the logratio function (as this transition kernel is symmetric), but we defined it so that the user can see an example of it.¹ Let’s take a look at the object:

kernel_unif_int
#> 
#> An environment of class fmcmc_kernel:
#> 
#> logratio : function (env)  
#> proposal : function (env)

The object itself is an R environment. If we added more parameters to kernel_new, we would have seen those as well. Now that we have our transition kernel, let’s give it a first try with the MCMC function.

ans <- MCMC(
  ll,                        # The log-likleihood function
  initial = max(y),          # A fair initial guess
  kernel  = kernel_unif_int, # Our new kernel function
  nsteps  = 1000,            # 1,000 MCMC draws
  thin    = 10,              # We will sample every 10
  p.      = p                # Passing extra parameters to be used by `ll`.
  )

Notice that for the initial guess, we are using the max of y', which is a reasonable starting point (the $N$ parameter MUST be at least the max ofy’). Since the returning object is an object of class mcmc from the coda R package, we can use any available method. Let’s start by plotting the chain:

plot(ans)

As you can see, the trace of the parameter started to go up right away, and then stayed around 500, the actual population parameter $N$. As the first part of the chain is useless (we are essentially moving away from the starting point); it is wise (if not necessary) to start the MCMC chain from the last point of ans. We can easily do so by just passing ans as a starting point, since MCMC will automatically take the last value of the chain as the starting point of this new one. This time, let’s increase the sample size as well:

ans <- MCMC(
  ll,
  initial = ans,             # MCMC will use tail(ans, 0) automatically
  kernel  = kernel_unif_int, # same as before
  nsteps  = 10000,           # More steps this time
  thin    = 10,              # same as before
  p.      = p                # same as before
)

Let’s take a look at the posterior distribution:

plot(ans)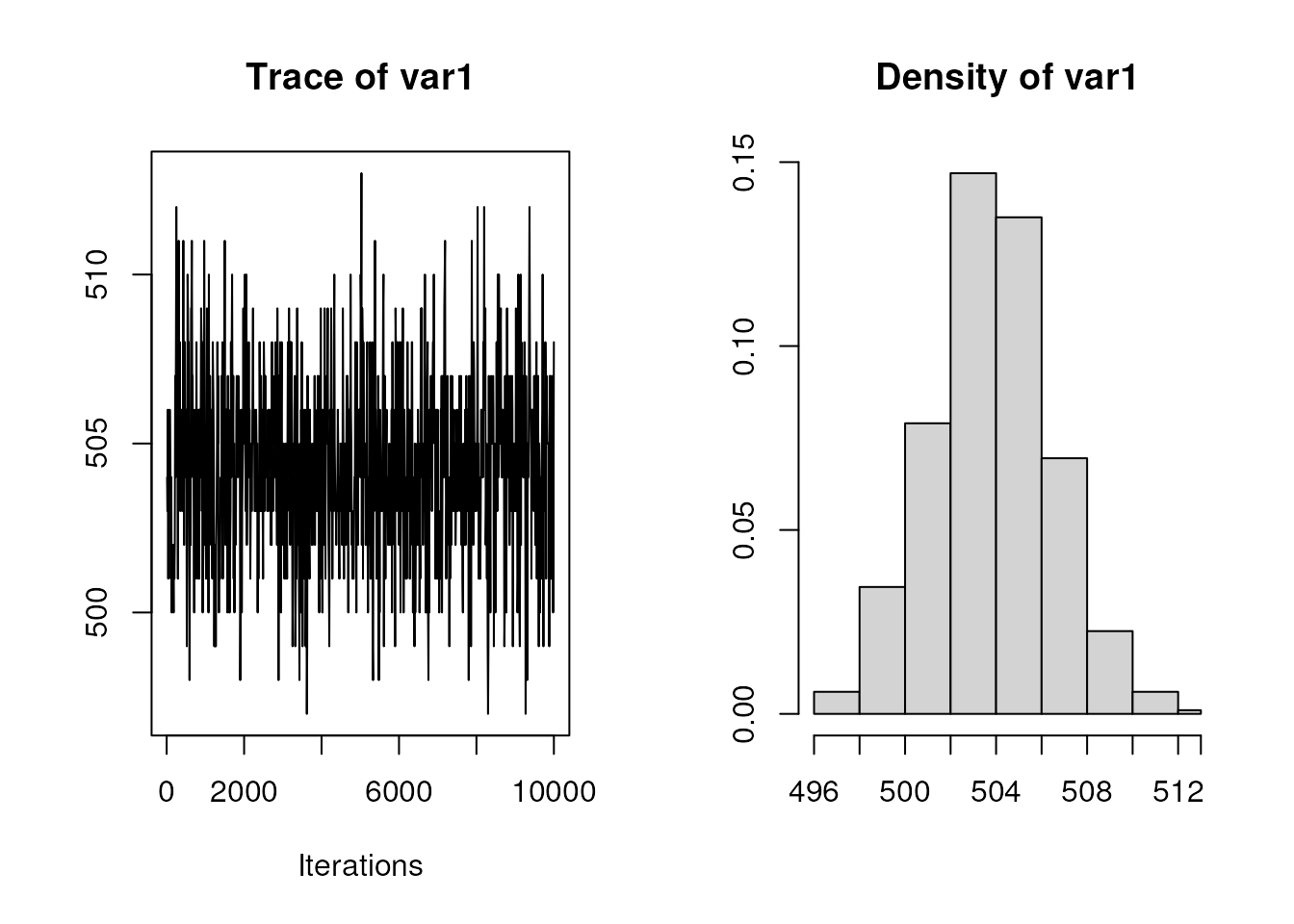

summary(ans)
#> 
#> Iterations = 10:10000
#> Thinning interval = 10 
#> Number of chains = 1 
#> Sample size per chain = 1000 
#> 
#> 1. Empirical mean and standard deviation for each variable,
#>    plus standard error of the mean:
#> 
#>           Mean             SD       Naive SE Time-series SE 
#>      504.30500        2.67902        0.08472        0.09960 
#> 
#> 2. Quantiles for each variable:
#> 
#>  2.5%   25%   50%   75% 97.5% 
#>   499   503   504   506   510
table(ans)
#> ans
#> 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 
#>   3   9  25  44  69  89 144 150 143 127  82  57  28  17   8   4   1

A very lovely mixing (at least visually) and a posterior distribution from which we can safely sample parameters.

For more details on what the env object contains, see the manual page of kernel_new.↩︎

George G. Vega Yon

2023-09-18

Introduction

Size parameter in a binomial distribution